4.3. VÍDEO TUTORIAL DE ROUTH-HURWITZ

Vídeo Tutorial de Routh-Hurwitz

Read more »

4.2. CASOS ESPECIALES DEL CRITERIO DE ROUTH-HURWITZ

Casos Especiales:

Si el término de la primera columna de cualquier renglón es cero, pero los términos restantes no son cero, o no hay términos restantes, el término cero se sustituye con un número positivo muy pequeño  ε  y se evalúa el resto del arreglo.

Ejemplo 3:

Considere la ecuación:

El arreglo de coeficientes es:

Si el signo del coeficiente que está encima del cero (ε) es igual al signo que está abajo de él, quiere decir que hay un par de raíces imaginarias.

Ejemplo 4:

Si  todos los coeficientes de cualquier renglón son cero significa que existen raíces con magnitudes iguales y signos  opuestos  y/o  dos  raíces  imaginarias  conjugadas.  En  este  caso,  la  evaluación  del  resto  del  arreglo continúa mediante la formación de un polinomio auxiliar con los coeficientes del último renglón y mediante el  empleo  de  los  coeficientes  de  la  derivada  de  este  polinomio  en  el  renglón  siguiente.  Tales  raíces se encuentran despejando el polinomio auxiliar, que siempre es par. Para un polinomio auxiliar de grado n 2, existen n pares de raíces iguales y opuestas. Por ejemplo, considere la ecuación:

El arreglo de coeficientes es:

Todos  los  términos  del  renglón s^3   son  cero.  Después  se  forma  el  polinomio  auxiliar  a  partir  de  los coeficientes del renglón s^4  El polinomio auxiliar  P(s ) es

lo  cual  indica  que  hay  dos  pares  de  raíces  de  igual  magnitud  y  signo  opuesto.  Estos pares  se  obtienen resolviendo la ecuación del polinomio auxiliar  P(s)= 0 . La derivada de  P(s) con respecto a  s  es

Los coeficientes de la última ecuación, sustituyen los términos del renglón 3 del arreglo. Por consiguiente, el arreglo de coeficientes se convierte en

No existen cambios de signo en la primera columna, no hay raíces con parte real positiva, sin embargo si hay raíces imaginarias.

Despejando las raíces del polinomio auxiliar

Obtenemos

Ejemplo 5:

Determine el rango de valores de  K  para la estabilidad.

La ecuación característica es:

El arreglo de coeficientes se convierte en:

Para  la  estabilidad,  K   debe  ser  positiva,  y  todos  los  coeficientes  de  la  primera  columna  deben  de  serlo también.

Por tanto, para que el sistema de control sea estable, el rango de  K  sería.

Cuando  600 = K ,  el  sistema  se  vuelve  oscilatorio  y, matemáticamente, la  oscilación  se mantiene  en  una amplitud constante.

Ejemplo 6:

Determine la estabilidad para siguiente sistema

La ecuación característica es

El arreglo de coeficientes se convierte en

Como  el  signo  arriba  y  abajo de  ε   son diferentes,  existen dos  cambios de  signo  en  los  coeficientes de  la primera columna, hay dos raíces con parte real positiva, el sistema es inestable.

Ejemplo 7:

Determine la estabilidad para siguiente sistema

La ecuación característica es:

El arreglo de coeficientes es

Todos  los  términos  del  renglón S^1 son cero. Entonces se forma el polinomio auxiliar a partir  de los coeficientes del renglón S^2 El polinomio auxiliar P(S) es.

Lo cual indica que hay dos raíces de igual magnitud y signo opuesto. La derivada de  P(s)  con respecto a s es.

Los coeficientes del renglón S^1 de la ecuación, se sustituyen por el polinomio determinado. Por consiguiente, el arreglo de coeficientes se convierte en

Existen dos cambios de signo en la primera columna, hay dos raíces con parte real positiva. Pero también existen raíces  imaginarias por el cero que se formó en el renglón S^1. Despejando las raíces del polinomio auxiliar.

Obtenemos las dos raíces imaginarias

Read more »

5. ERROR EN ESTADO ESTABLE

Error en Estado Estacionario:

El error en estado estacionario es una medida de la exactitud de un sistema de control para seguir una entrada dada, después de desaparecer la respuesta transitoria. Se analizará el error en estado estacionario provocado por  la incapacidad del sistema de seguir determinados tipos de entradas.

El  que  un  sistema  dado  presente  o  no  un  error  en  estado  estacionario  ante  determinado  tipo  de  señal  de entrada, depende del tipo de función de transferencia de lazo abierto del sistema.

Clasificación de los sistemas de control

Los  sistemas  de  control  se  clasifican  de  acuerdo  con  su  capacidad  de  seguir  entradas  escalón,  rampa, parábola,  etc.  Considere  el  sistema  de  control  con  realimentación  unitaria  con  la  siguiente  función  de transferencia en lazo abierto G(s):

Este sistema contiene el término s^N en el denominador, que representa un polo de multiplicidad N en el origen. El esquema de clasificación se basa en la cantidad de integraciones (términos  s 1 ) indicadas por la función de transferencia en  lazo abierto. Un sistema se denomina de tipo 0, si N = 0, de tipo 1, si N = 1, de tipo 2, si N = 2,…etc.

Ejemplo: 

Error en estado estacionario:

El error en un sistema de control es la diferencia entre el valor deseado r(t) y el valor actual c(t), de la variable controlada.

El error en estado estacionario es aquel error que permanece después de que ha desaparecido el transitorio.

Puede observarse de que el error depende:

•     De la entrada: R(S)
•     De las características del sistema de lazo abierto GH(S)

Para el siguiente sistema de control, la función de transferencia de lazo cerrado es

El error en estado estacionario es

Sistemas con realimentación unitaria:

Estos sistemas tienen un diagrama en bloques como el indicado en la fig. En ellos la señal de referencia y la de entrada coinciden o sea: SR(s)= R(s):

En general cualquier función transferencia puede ser escrita como:

Para los sistemas de realimentación unitaria el “tipo de sistema” se define según sea el valor de “n” en la expresión anterior. Es decir según el número de integraciones puras en la cadena directa.

Ejemplo:

El tipo de sistema indica que orden de señales de referencia puede “seguir” un sistema con error nulo en régimen estacionario. Aquí “el orden” se refiere a la potencia de s en la transformada de Laplace de la referencia. Para ver esto, 

investigaremos el error en estacionario para varios tipos de sistemas, debido a las señales de referencia: impulso R(s)=1, escalón R(s)=1/s, rampa R(s)=1/s∧2 y parábola R(s)=1/s∧3. 

El error para el sistema de realimentación unitaria, se obtiene como: 

En régimen permanente, el error se obtiene aplicando el teorema del valor final, de la transformada de Laplace:

1.- Entrada Impulso: R(s)=1:

Sistema Tipo “0”: 

Sistema tipo “1”:

Sistema tipo “2” y superiores:

2.-Entrada escalón R(s)=1/s:


Sistema Tipo “0”:

Sistemas Tipo “1” y mayores:

3.- Entrada rampa R(s)=1/s∧2: 

Sistema tipo “0”

Sistema Tipo “1”

Sistema Tipo “2” y superiores

4.-Entrada parábola R(s)=1/s∧3: 

Sistema Tipo “0”, 

Sistema Tipo “1”, 

Sistema tipo “2”, 

Sistema tipo “3” y superiores

Read more »

4.1. CRITERIO DE ESTABILIDAD DE ROUTH-HURWITZ

Introducción:

Routh (1874) propuso un criterio legendario para saber si Un polinomio como:

Tiene todas sus raíces en el semiplano izquierdo, o no. El Criterio resulta de plantear un arreglo de coeficientes, con Forma triangular, y de observar si la primera columna tiene Todos sus coeficientes con signos iguales, o no.

El Arreglo:

El arreglo se construye de la manera siguiente:

Las dos filas superiores se construyen de modo obvio, con los coeficientes del polinomio; las otras filas se construyen paulatinamente mediante el procedimiento insinuado enseguida:

El problema más importante de los sistemas de control lineal tiene que ver con la estabilidad. Un sistema de control  es  estable  si  y  sólo  si  todos  los polos  en  lazo  cerrado  se  encuentran  en  el  semiplano  izquierdo  del plano s.

Consideremos la siguiente función de transferencia de lazo cerrado. 

En donde las a y las b son constantes y  n m ≤ .

Criterio de estabilidad de Routh: 

El criterio de estabilidad de Routh permite determinar la cantidad de polos en lazo cerrado que se encuentran en el semiplano derecho del plano  s  (raíces positivas) sin tener que factorizar el polinomio. Este criterio de estabilidad sólo se aplica a los polinomios con una cantidad finita de términos.

Procedimiento en el criterio de estabilidad de Routh:

1. Escriba el polinomio en  s del denominador en la forma siguiente: 

En donde  los coeficientes son cantidades reales. Suponemos que  0 ≠ n a ; es decir, se elimina cualquier raíz cero.

2. Si alguno de los coeficientes es cero o negativo, ante la presencia de al menos un coeficiente positivo, hay una raíz, o raíces imaginarias o que tiene partes reales positivas. En tal caso, el sistema no es estable. La  condición necesaria,  pero no  suficiente, para  la  estabilidad  es que  todos  los  coeficientes de  la  ecuación estén presentes y tengan signo positivo.

3. Si todos  los coeficientes son positivos, ordene los coeficientes del polinomio en renglones y columnas de acuerdo con el patrón o arreglo siguiente:

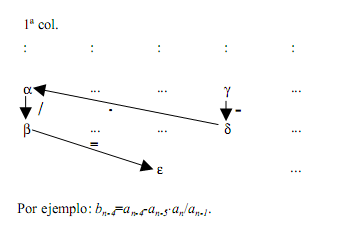
Los coeficientes  b1,b2,b3,…,c1,c2,c3,….,d1,d2,…,  etc., se evalúan del modo siguiente: 

La evaluación continúa hasta que todas las restantes son cero. 

El criterio de estabilidad de Routh- Hurwitz plantea que el número de raíces de la ecuación con partes reales positivas es igual al número de cambios de signo de los coeficientes de la primera columna del arreglo. 

La condición necesaria y  suficiente para que  todas  las  raíces de  la ecuación  se encuentren en el semiplano izquierdo del plano  s  es que todos los coeficientes de la ecuación sean positivos y que todos los términos de la primera columna del arreglo tengan signo positivo. 

Ejemplo 1:

Considere el polinomio siguiente:

Los primeros dos renglones se obtienen directamente del polinomio dado. El arreglo de coeficientes sería

Hay dos cambios de signo en los coeficientes de la primera columna. Esto significa que existen dos raíces con partes reales positivas. Observe que el resultado no se modifica cuando los coeficientes de cualquier renglón se multiplican por, o se dividen entre, un número positivo para simplificar el cálculo.

Ejemplo 2:

Aplicación del criterio de estabilidad de Routh al análisis de un sistema de control. Considere  el  sistema de  la  figura. Determine  el  rango de valores  de  K  para  la  estabilidad. La  función de transferencia en lazo cerrado es

La ecuación característica es

El arreglo de coeficientes se convierte en

Para  la  estabilidad,  K  debe  ser  positiva,  y  todos  los  coeficientes  de  la  primera  columna  deben  de  serlo también

Por tanto, para que el sistema de control sea estable, el rango de K sería

Cuando K= 14/9,  el Coeficiente  de  la  primer  columna  de  la  fila 1 s se  hace  cero,  esto  significa que  existen raíces  imaginarias y  el  sistema  se vuelve  oscilatorio  y, matemáticamente,  la oscilación  se mantiene  en una amplitud constante.

Se pueden calcular las raíces imaginarias, considerando un polinomio auxiliar el cuál se obtiene tomando los coeficientes de la fila que se encuentra arriba donde se generó el cero. La ecuación sería

Read more »