Indice de Clases:
Itroduccion a los Sistemas de Control
sistemas de control en Lazo Cerrado
Sistemas de control en Lazo Abierto
Comparación entre Lazos
Funcionesde Transferencia
Diagramas de Bloques - Algebra de Bloques
Diagramas de Flujo de Señal - Diagramas de Mason
Criterio de Estabilidad de ROUTH-HURWITZ
CasosEspeciales del Criterio de ROUTH-HURWITZ
Vídeo Tutorial de Routh-Hurwitz
Error en Estado Estable
1. INTRODUCCIÓN A LOS SISTEMAS DE CONTROL
¿QUÉ ES UN SISTEMA DE CONTROL?
Los sistemas de control están formados por un conjunto de dispositivos de diversa naturaleza (mecánicos, eléctricos, electrónicos, neumáticos, hidráulicos) cuya finalidad es controlar el funcionamiento de una máquina o de un proceso.
En todo sistema de control podemos considerar una señal de entrada que actúa sobre el mismo y una señal de salida proporcionada por el sistema, según el siguiente esquema:
Un sistema dinámico puede definirse conceptualmente como un ente que recibe unas acciones externas o variables de entrada, y cuya respuesta a estas acciones externas son las denominadas variables de salida.
Las acciones externas al sistema se dividen en dos grupos, variables de control, que se pueden manipular, y perturbaciones sobre las que no es posible ningún tipo de control.
La Figura ilustra de un modo conceptual el funcionamiento de un sistema.
Dentro de los sistemas se encuentra el concepto de sistema de control. Un sistema de control es un tipo de sistema que se caracteriza por la presencia de una serie de elementos que permiten influir en el funcionamiento del sistema. La finalidad de un sistema de control es conseguir, mediante la manipulación de las variables de control, un dominio sobre las variables de salida, de modo que estas alcancen unos valores prefijados (consigna).
Un sistema de control ideal debe ser capaz de conseguir su objetivo cumpliendo los siguientes requisitos:
1. Garantizar la estabilidad y, particularmente, ser robusto frente a perturbaciones y errores en los modelos.
3. Ser fácilmente implementable y cómodo de operar en tiempo real con ayuda de un ordenador.
Los elementos básicos que forman parte de un sistema de control y permiten su manipulación son los siguientes:
- Sensores. Permiten conocer los valores de las variables medidas del sistema.
- Controlador. Utilizando los valores determinados por los sensores y la consigna impuesta, calcula la acción que debe aplicarse para modificar las variables de control en base a cierta estrategia.
- Actuador. Es el mecanismo que ejecuta la acción calculada por el controlador y que modifica las variables de control.
2.1 Sistemas de control en lazo cerrado:
Sistemas de control realimentados o control en lazo cerrado:
Un sistema que mantiene una relación prescrita entre la salida y la entrada de referencia, comparándolas y usando la diferencia como, se denomina sistema de control realimentado.
Un ejemplo sería el sistema de control de temperatura de una habitación. Midiendo la temperatura real y comparándola con la temperatura de referencia (la temperatura deseada), el termostato activa o desactiva el equipo de calefacción o de enfriamiento para asegurar que la temperatura, de la habitación se conserve en un nivel cómodo sin considerar las condiciones externas.
Los sistemas de control realimentados no se limitan a la ingeniería, sino que también se encuentran en diversos campos ajenos a ella. Por ejemplo, el cuerpo humano es un sistema de control realimentado muy avanzado tanto la temperatura corporal como la presión sanguínea se conservan constantes mediante una realimentación fisiológica. De hecho, la realimentación realiza una función vital: vuelve el cuerpo humano relativamente insensible a las perturbaciones externas, por lo cual lo habilita para funcionar en forma adecuada en un ambiente cambiante.
Los sistemas de control realimentados se denominan también sistemas de control en lazo cerrado. En la práctica, los términos control realimentado y control en lazo cerrado se usan indistintamente.
En un sistema de control en lazo cerrado, se alimenta al controlador la señal de error de actuación, que es la diferencia entre la señal de entrada y la señal de realimentación (que puede ser la señal de salida misma o una función de la señal de salida y sus derivadas y/o integrales), a fin de reducir el error y llevar la salida del sistema a un valor conveniente. El término control en lazo cerrado siempre implica el uso de una acción de control realimentado para reducir el error del sistema.
2.2 Sistemas de control en lazo abierto:
2.2 Sistemas de control en lazo abierto:
Sistemas de control en lazo abierto
Los sistemas en los cuales la salida no afecta la acción de control se denominan sistemas de control en lazo abierto.
En otras palabras, en un sistema de control en lazo abierto no se mide la salida ni se realimenta para comparar la con la entrada. Un ejemplo práctico es una lavadora. El remojo, el lavado y el enjuague en la lavadora operan con una base de tiempo. La máquina no mide la señal de salida, que es la limpieza de la ropa.
En cualquier sistema de control en lazo abierto, la salida no se compara con la entrada de referencia. Por tanto, a cada entrada de referencia le corresponde una condición operativa fija; como resultado, la precisión del sistema depende de la calibración. Ante la presencia de perturbaciones, un sistema de control en lazo abierto no realiza la tarea deseada.
En La práctica, el control en lazo abierto sólo se usa si se conoce la relación entre la entrada y la salida y si no hay perturbaciones internas ni externas. Es evidente que estos sistemas no son de control realimentado.
Observe que cualquier sistema de control que opere con una base de tiempo es en lazo abierto. Por ejemplo, el control del tránsito mediante señales operadas con una base de tiempo es otro ejemplo de control en lazo abierto.
2.3 Comparación entre Lazos:
Sistemas de control en lazo cerrado en comparación con los sistemas en lazo abierto
Una ventaja del sistema de control en lazo cerrado es que el uso de la realimentación vuelve la respuesta del sistema relativamente insensible a las perturbaciones externas y a las variaciones internas en los parámetros del sistema. Por tanto, es posible usar componentes relativamente precisos y baratos para obtener el control adecuado de una planta determinada, en tanto que hacer eso es imposible en el caso de un sistema en lazo abierto.
Desde el punto de vista de la estabilidad, el sistema de control en lazo abierto es más fácil de desarrollar, porque la estabilidad del sistema no es un problema importante. Por otra parte, la estabilidad es una función principal en el sistema de control en lazo cerrado, lo cual puede conducir a corregir en exceso errores que producen oscilaciones de amplitud constante o cambiante.
Debe señalarse que, para los sistemas en los que se conocen con anticipación las entradas y en los cuales no hay perturbaciones, es aconsejable emplear un control en lazo abierto. Los sistemas de control en lazo cerrado sólo tienen ventajas cuando se presentan perturbaciones impredecibles y/o variaciones impredecibles en los componentes del sistema.
Observe que la valoración de la energía de salida determina en forma parcial el costo, el peso y el tamaño de un sistema de control. La cantidad de componentes usados en un sistema de control en lazo cerrado es mayor que la que se emplea para un sistema de control equivalente en lazo abierto. Por tanto, el sistema de control en lazo cerrado suele tener costos y potencias más grandes. Para disminuir la energía requerida de un sistema, se emplea un control en lazo abierto cuando puede aplicarse. Por lo general, una combinación adecuada de controles en lazo abierto y en lazo cerrado es menos costosa y ofrecerá un desempeño satisfactorio del sistema general.
3.1 FUNCIONES DE TRANSFERENCIA
En la teoría de control, a menudo se usan las funciones de transferencia para caracterizar las relaciones de entrada-salida de componentes o de sistemas que se describen mediante ecuaciones diferenciales lineales invariantes con el tiempo. Empezaremos por definir la función de transferencia y proseguiremos con una derivación de la función de transferencia de un sistema mecánico.
La función de transferencia de un sistema descrito mediante una ecuación diferencial lineal e invariante con el tiempo se define como el cociente entre la transformada de Laplace de la salida (función de respuesta) y la transformada de Laplace de la entrada (función de excitación) bajo la suposición de que todas las condiciones iniciales son cero.
Considere el sistema lineal e invariante con el tiempo descrito mediante la siguiente ecuación diferencial:
En donde y es la salida del sistema y x es la entrada. La función de transferencia de este sistema se obtiene tomando la transformada de Laplace de ambos miembros de la ecuación bajo la suposición de que todas las condiciones iniciales son cero, o bien.
A partir del concepto de función de transferencia, es posible representar la dinámica de un sistema mediante ecuaciones algebraicas en s. Si la potencia más alta de s en el denominador de la función de transferencia es igual a >t, el sistema se denomina sistema de n-ésimo orden.
La aplicación del concepto de función de transferencia está limitada a los sistemas descritos mediante ecuaciones diferenciales lineales invariantes con el tiempo. Sin embargo, el enfoque de la función de transferencia se usa extensamente en el análisis y diseño de dichos sistemas.
A continuación se presentan algunos comentarios importantes relacionados con la función de transferencia. (Observe que, en la lista, los sistemas a los que se hace referencia son aquellos que se describen mediante una ecuación diferencial lineal e invariante con el tiempo.)
1. La función de transferencia de un sistema es un modelo matemático porque es un método operacional para expresar la ecuación diferencial que relaciona la variable de salida con la variable de entrada.
2. La función de transferencia es una propiedad de un sistema, independiente de la magnitud y naturaleza de la entrada o función de excitación.
3. La función de transferencia incluye las unidades necesarias para relacionar la entrada con la salida; sin embargo, no proporciona información acerca de la estructura física del sistema. (Las funciones de transferencia de muchos sistemas físicamente diferentes pueden ser idénticas.)
4. Si se conoce la función de transferencia de un sistema, se estudia la salida o respuesta
para varias formas de entrada, con la intención de comprender la naturaleza del sistema.
5. Si se desconoce la función de transferencia de un sistema, puede establecerse experimentalmente introduciendo entradas conocidas y estudiando la salida del sistema. Una vez establecida una función de transferencia, proporciona una descripción completa de las características dinámicas del sistema, a diferencia de su descripción física.
DIAGRAMAS DE BLOQUES - ÁLGEBRA DE BLOQUES
Diagramas de Bloque
Diagramas de Bloque
A partir de la definición de función de transferencia de un sistema SISO, resulta ser conveniente una descripción gráfica de los sistemas. Una de dichas representaciones gráficas es la que denominamos diagramas de bloques. En ella las funciones de transferencia se representan mediante un bloque (un rectángulo en cuyo interior se describe la función de transferencia), del cual ingresa (flecha en el sentido hacia el bloque) la señal de entrada, y sale (flecha en el sentido hacia afuera del bloque) la salida que será el producto de la función de transferencia por la entrada:
Para completar los diagramas de bloques de los sistemas hace falta incorporar un nuevo elemento: los sumadores. En el mismo, todas las señales ingresantes son sumadas con su respectivo signo para dar como resultado la salida:
Así los sistemas pueden ser descriptos gráficamente a través de diagramas de bloques. Estos diagramas de bloques pueden ser reducidos utilizando el algebra de bloques para obtener un solo bloque total en el cual se describa la función de transferencia entre la entrada del sistema a la salida del sistema. A continuación veremos en que consiste este algebra de bloques.
En particular, las funciones de transferencia que consisten en directamente multiplicar la entrada por una constante se las llaman directamente ganancias, y suelen dibujarse como triángulos:
Reducción de los diagramas de bloques
Podemos encontrar diversos sistemas de control, representados con diagramas de bloques complejos. Dichos diagramas los podemos reducir a un simple bloque empleando las siguientes reglas:
Bloques en serie:
Bloques en paralelo:
Bloques en realimentación:
Equivalencias en el álgebra de bloques:
Ejemplo:
Tenemos el diagrama de bloques de la siguiente figura, el cual queremos reducir.
Utilizando la reducción del lazo interno G1-G3 el diagrama queda:
Transladando de lugar la señal entrante al bloque G6:
Finalmente, de la figura que es una retroalimentación en serie con unos bloques en paralelo, obtenemos la función de transferencia G(s) = Y(s)/R(s):
4.1. CRITERIO DE ESTABILIDAD DE ROUTH-HURWITZ
Introducción:
Tiene todas sus raíces en el semiplano izquierdo, o no. El Criterio resulta de plantear un arreglo de coeficientes, con Forma triangular, y de observar si la primera columna tiene Todos sus coeficientes con signos iguales, o no.
El Arreglo:
El arreglo se construye de la manera siguiente:
Las dos filas superiores se construyen de modo obvio, con los coeficientes del polinomio; las otras filas se construyen paulatinamente mediante el procedimiento insinuado enseguida:
El problema más importante de los sistemas de control lineal tiene que ver con la estabilidad. Un sistema de control es estable si y sólo si todos los polos en lazo cerrado se encuentran en el semiplano izquierdo del plano s.
Consideremos la siguiente función de transferencia de lazo cerrado.
En donde las a y las b son constantes y n m ≤ .
Criterio de estabilidad de Routh:
El criterio de estabilidad de Routh permite determinar la cantidad de polos en lazo cerrado que se encuentran en el semiplano derecho del plano s (raíces positivas) sin tener que factorizar el polinomio. Este criterio de estabilidad sólo se aplica a los polinomios con una cantidad finita de términos.
Procedimiento en el criterio de estabilidad de Routh:
1. Escriba el polinomio en s del denominador en la forma siguiente:
En donde los coeficientes son cantidades reales. Suponemos que 0 ≠ n a ; es decir, se elimina cualquier raíz cero.
2. Si alguno de los coeficientes es cero o negativo, ante la presencia de al menos un coeficiente positivo, hay una raíz, o raíces imaginarias o que tiene partes reales positivas. En tal caso, el sistema no es estable. La condición necesaria, pero no suficiente, para la estabilidad es que todos los coeficientes de la ecuación estén presentes y tengan signo positivo.
3. Si todos los coeficientes son positivos, ordene los coeficientes del polinomio en renglones y columnas de acuerdo con el patrón o arreglo siguiente:
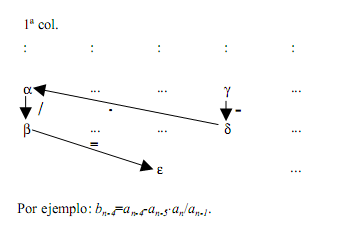
Los coeficientes b1,b2,b3,…,c1,c2,c3,….,d1,d2,…, etc., se evalúan del modo siguiente:
La evaluación continúa hasta que todas las restantes son cero.
El criterio de estabilidad de Routh- Hurwitz plantea que el número de raíces de la ecuación con partes reales positivas es igual al número de cambios de signo de los coeficientes de la primera columna del arreglo.
La condición necesaria y suficiente para que todas las raíces de la ecuación se encuentren en el semiplano izquierdo del plano s es que todos los coeficientes de la ecuación sean positivos y que todos los términos de la primera columna del arreglo tengan signo positivo.
Ejemplo 1:
Considere el polinomio siguiente:
Los primeros dos renglones se obtienen directamente del polinomio dado. El arreglo de coeficientes sería
Hay dos cambios de signo en los coeficientes de la primera columna. Esto significa que existen dos raíces con partes reales positivas. Observe que el resultado no se modifica cuando los coeficientes de cualquier renglón se multiplican por, o se dividen entre, un número positivo para simplificar el cálculo.
Ejemplo 2:
Aplicación del criterio de estabilidad de Routh al análisis de un sistema de control. Considere el sistema de la figura. Determine el rango de valores de K para la estabilidad. La función de transferencia en lazo cerrado es
La ecuación característica es
El arreglo de coeficientes se convierte en
Para la estabilidad, K debe ser positiva, y todos los coeficientes de la primera columna deben de serlo también
Por tanto, para que el sistema de control sea estable, el rango de K sería
Cuando K= 14/9, el Coeficiente de la primer columna de la fila 1 s se hace cero, esto significa que existen raíces imaginarias y el sistema se vuelve oscilatorio y, matemáticamente, la oscilación se mantiene en una amplitud constante.
Se pueden calcular las raíces imaginarias, considerando un polinomio auxiliar el cuál se obtiene tomando los coeficientes de la fila que se encuentra arriba donde se generó el cero. La ecuación sería
4.2. CASOS ESPECIALES DEL CRITERIO DE ROUTH-HURWITZ
Casos Especiales:
Casos Especiales:
Si el término de la primera columna de cualquier renglón es cero, pero los términos restantes no son cero, o no hay términos restantes, el término cero se sustituye con un número positivo muy pequeño ε y se evalúa el resto del arreglo.
Ejemplo 3:
Considere la ecuación:
El arreglo de coeficientes es:
Si el signo del coeficiente que está encima del cero (ε) es igual al signo que está abajo de él, quiere decir que hay un par de raíces imaginarias.
Ejemplo 4:
Si todos los coeficientes de cualquier renglón son cero significa que existen raíces con magnitudes iguales y signos opuestos y/o dos raíces imaginarias conjugadas. En este caso, la evaluación del resto del arreglo continúa mediante la formación de un polinomio auxiliar con los coeficientes del último renglón y mediante el empleo de los coeficientes de la derivada de este polinomio en el renglón siguiente. Tales raíces se encuentran despejando el polinomio auxiliar, que siempre es par. Para un polinomio auxiliar de grado n 2, existen n pares de raíces iguales y opuestas. Por ejemplo, considere la ecuación:
El arreglo de coeficientes es:
Todos los términos del renglón s^3 son cero. Después se forma el polinomio auxiliar a partir de los coeficientes del renglón s^4 El polinomio auxiliar P(s ) es
lo cual indica que hay dos pares de raíces de igual magnitud y signo opuesto. Estos pares se obtienen resolviendo la ecuación del polinomio auxiliar P(s)= 0 . La derivada de P(s) con respecto a s es
Los coeficientes de la última ecuación, sustituyen los términos del renglón 3 del arreglo. Por consiguiente, el arreglo de coeficientes se convierte en
No existen cambios de signo en la primera columna, no hay raíces con parte real positiva, sin embargo si hay raíces imaginarias.
Despejando las raíces del polinomio auxiliar
Obtenemos
Ejemplo 5:
Determine el rango de valores de K para la estabilidad.
La ecuación característica es:
El arreglo de coeficientes se convierte en:
Para la estabilidad, K debe ser positiva, y todos los coeficientes de la primera columna deben de serlo también.
Por tanto, para que el sistema de control sea estable, el rango de K sería.
Cuando 600 = K , el sistema se vuelve oscilatorio y, matemáticamente, la oscilación se mantiene en una amplitud constante.
Ejemplo 6:
Determine la estabilidad para siguiente sistema
El arreglo de coeficientes se convierte en
Como el signo arriba y abajo de ε son diferentes, existen dos cambios de signo en los coeficientes de la primera columna, hay dos raíces con parte real positiva, el sistema es inestable.
Ejemplo 7:
Determine la estabilidad para siguiente sistema
Todos los términos del renglón S^1 son cero. Entonces se forma el polinomio auxiliar a partir de los coeficientes del renglón S^2 El polinomio auxiliar P(S) es.
Lo cual indica que hay dos raíces de igual magnitud y signo opuesto. La derivada de P(s) con respecto a s es.
Los coeficientes del renglón S^1 de la ecuación, se sustituyen por el polinomio determinado. Por consiguiente, el arreglo de coeficientes se convierte en
Existen dos cambios de signo en la primera columna, hay dos raíces con parte real positiva. Pero también existen raíces imaginarias por el cero que se formó en el renglón S^1. Despejando las raíces del polinomio auxiliar.
Obtenemos las dos raíces imaginarias
Vídeo Tutorial de Routh-Hurwitz
5. ERROR EN ESTADO ESTABLE
Error en Estado Estacionario:
El error en estado estacionario es una medida de la exactitud de un sistema de control para seguir una entrada dada, después de desaparecer la respuesta transitoria. Se analizará el error en estado estacionario provocado por la incapacidad del sistema de seguir determinados tipos de entradas.
El que un sistema dado presente o no un error en estado estacionario ante determinado tipo de señal de entrada, depende del tipo de función de transferencia de lazo abierto del sistema.
Clasificación de los sistemas de control
Los sistemas de control se clasifican de acuerdo con su capacidad de seguir entradas escalón, rampa, parábola, etc. Considere el sistema de control con realimentación unitaria con la siguiente función de transferencia en lazo abierto G(s):
Este sistema contiene el término s^N en el denominador, que representa un polo de multiplicidad N en el origen. El esquema de clasificación se basa en la cantidad de integraciones (términos s 1 ) indicadas por la función de transferencia en lazo abierto. Un sistema se denomina de tipo 0, si N = 0, de tipo 1, si N = 1, de tipo 2, si N = 2,…etc.
Ejemplo:
Error en estado estacionario:
El error en un sistema de control es la diferencia entre el valor deseado r(t) y el valor actual c(t), de la variable controlada.
El error en estado estacionario es aquel error que permanece después de que ha desaparecido el transitorio.
Puede observarse de que el error depende:
- De la entrada: R(S)
- De las características del sistema de lazo abierto GH(S)
Para el siguiente sistema de control, la función de transferencia de lazo cerrado es
El error en estado estacionario es
Sistemas con realimentación unitaria:
Estos sistemas tienen un diagrama en bloques como el indicado en la fig. En ellos la señal de referencia y la de entrada coinciden o sea: SR(s)= R(s):
En general cualquier función transferencia puede ser escrita como:
Para los sistemas de realimentación unitaria el “tipo de sistema” se define según sea el valor de “n” en la expresión anterior. Es decir según el número de integraciones puras en la cadena directa.
Ejemplo:
El tipo de sistema indica que orden de señales de referencia puede “seguir” un sistema con error nulo en régimen estacionario. Aquí “el orden” se refiere a la potencia de s en la transformada de Laplace de la referencia. Para ver esto,
investigaremos el error en estacionario para varios tipos de sistemas, debido a las señales de referencia: impulso R(s)=1, escalón R(s)=1/s, rampa R(s)=1/s∧2 y parábola R(s)=1/s∧3.
El error para el sistema de realimentación unitaria, se obtiene como:
En régimen permanente, el error se obtiene aplicando el teorema del valor final, de la transformada de Laplace:
1.- Entrada Impulso: R(s)=1:
Sistema Tipo “0”:
Sistema tipo “1”:
Sistema tipo “2” y superiores:
2.-Entrada escalón R(s)=1/s:
Sistema Tipo “0”:
Sistemas Tipo “1” y mayores:
3.- Entrada rampa R(s)=1/s∧2:
Sistema tipo “0”
Sistema Tipo “1”
Sistema Tipo “2” y superiores
4.-Entrada parábola R(s)=1/s∧3:
Sistema Tipo “0”,
Sistema Tipo “1”,
Sistema tipo “2”,
Sistema tipo “3” y superiores























































































0 comentarios:
Publicar un comentario