4.1. CRITERIO DE ESTABILIDAD DE ROUTH-HURWITZ

Introducción:

Routh (1874) propuso un criterio legendario para saber si Un polinomio como:

Tiene todas sus raíces en el semiplano izquierdo, o no. El Criterio resulta de plantear un arreglo de coeficientes, con Forma triangular, y de observar si la primera columna tiene Todos sus coeficientes con signos iguales, o no.

El Arreglo:

El arreglo se construye de la manera siguiente:

Las dos filas superiores se construyen de modo obvio, con los coeficientes del polinomio; las otras filas se construyen paulatinamente mediante el procedimiento insinuado enseguida:

El problema más importante de los sistemas de control lineal tiene que ver con la estabilidad. Un sistema de control  es  estable  si  y  sólo  si  todos  los polos  en  lazo  cerrado  se  encuentran  en  el  semiplano  izquierdo  del plano s.

Consideremos la siguiente función de transferencia de lazo cerrado. 

En donde las a y las b son constantes y  n m ≤ .

Criterio de estabilidad de Routh: 

El criterio de estabilidad de Routh permite determinar la cantidad de polos en lazo cerrado que se encuentran en el semiplano derecho del plano  s  (raíces positivas) sin tener que factorizar el polinomio. Este criterio de estabilidad sólo se aplica a los polinomios con una cantidad finita de términos.

Procedimiento en el criterio de estabilidad de Routh:

1. Escriba el polinomio en  s del denominador en la forma siguiente: 

En donde  los coeficientes son cantidades reales. Suponemos que  0 ≠ n a ; es decir, se elimina cualquier raíz cero.

2. Si alguno de los coeficientes es cero o negativo, ante la presencia de al menos un coeficiente positivo, hay una raíz, o raíces imaginarias o que tiene partes reales positivas. En tal caso, el sistema no es estable. La  condición necesaria,  pero no  suficiente, para  la  estabilidad  es que  todos  los  coeficientes de  la  ecuación estén presentes y tengan signo positivo.

3. Si todos  los coeficientes son positivos, ordene los coeficientes del polinomio en renglones y columnas de acuerdo con el patrón o arreglo siguiente:

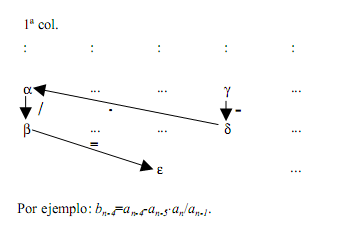
Los coeficientes  b1,b2,b3,…,c1,c2,c3,….,d1,d2,…,  etc., se evalúan del modo siguiente: 

La evaluación continúa hasta que todas las restantes son cero. 

El criterio de estabilidad de Routh- Hurwitz plantea que el número de raíces de la ecuación con partes reales positivas es igual al número de cambios de signo de los coeficientes de la primera columna del arreglo. 

La condición necesaria y  suficiente para que  todas  las  raíces de  la ecuación  se encuentren en el semiplano izquierdo del plano  s  es que todos los coeficientes de la ecuación sean positivos y que todos los términos de la primera columna del arreglo tengan signo positivo. 

Ejemplo 1:

Considere el polinomio siguiente:

Los primeros dos renglones se obtienen directamente del polinomio dado. El arreglo de coeficientes sería

Hay dos cambios de signo en los coeficientes de la primera columna. Esto significa que existen dos raíces con partes reales positivas. Observe que el resultado no se modifica cuando los coeficientes de cualquier renglón se multiplican por, o se dividen entre, un número positivo para simplificar el cálculo.

Ejemplo 2:

Aplicación del criterio de estabilidad de Routh al análisis de un sistema de control. Considere  el  sistema de  la  figura. Determine  el  rango de valores  de  K  para  la  estabilidad. La  función de transferencia en lazo cerrado es

La ecuación característica es

El arreglo de coeficientes se convierte en

Para  la  estabilidad,  K  debe  ser  positiva,  y  todos  los  coeficientes  de  la  primera  columna  deben  de  serlo también

Por tanto, para que el sistema de control sea estable, el rango de K sería

Cuando K= 14/9,  el Coeficiente  de  la  primer  columna  de  la  fila 1 s se  hace  cero,  esto  significa que  existen raíces  imaginarias y  el  sistema  se vuelve  oscilatorio  y, matemáticamente,  la oscilación  se mantiene  en una amplitud constante.

Se pueden calcular las raíces imaginarias, considerando un polinomio auxiliar el cuál se obtiene tomando los coeficientes de la fila que se encuentra arriba donde se generó el cero. La ecuación sería